Демонстрационный вариант ЕГЭ по математике 2016 года профильного уровня
17 Октябрь 2015
Просмотров:
3117
Демонстрационный вариант экзаменационной работы предназначен для того, чтобы дать школьнику представление о содержании и структуре работы, о том, сколько в ней будет заданий, в каком порядке расположены, как сформулированы и как требуется записать ответ. Вы можете потренироваться на этом варианте, обратив особое внимание на то, как авторы ЕГЭ подходят правильной к записи ответов и решений к заданиям.
Внимательно прочитайте пояснения, которые даются к демонстрационному варианту — оно содержит важную информацию, касающуюся оценки правильных ответов: сколько баллов дается за выполнение того или иного задания, какого минимальное количество выполненных заданий, сколько времени отводится на решение всей работы и т.п.
Вы можете скачать демонстрационный вариант ЕГЭ по математике 2016 профильного уровня в формате pdf:
Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2016 года по математике. Профильный уровень (pdf)
Или пройти первичное тестирование онлайн:
См. также:
- демонстрационные варианты 2017, 2018 годов профильного уровня с решением;
- демонстрационный вариант 2019 года профильного уровня с решением.
Задачи повышенного уровня сложности:
Задачи высокого уровня сложности:
Навигация
Предыдущая статья: ← Пробные и тренировочные ЕГЭ по математике профильного уровня
Следующая статья: Расписание ЕГЭ по математике 2016 →
Курс ЕГЭ по математике
Цены и условия
Статистика
Поддержка
© 2026 ЕГЭ по математике 2021 профильный уровень


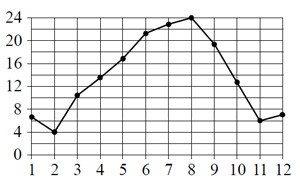 Сколько месяцев средняя
температура была больше 18 градусов Цельсия?
Сколько месяцев средняя
температура была больше 18 градусов Цельсия?