Демонстрационный вариант ЕГЭ по математике 2019 года профильного уровня с решением

8 Апрель 2019 Главная страница » ЕГЭ по математике Просмотров: 2394

Здесь представлен демонстрационный вариант экзаменационной работы профильного уровня 2019 года. По содержанию и структуре он не отличается от вариантов 2017 и 2018 годов, поэтому для подготовки к экзамену 2019 года рекомендуем Вам также ознакомиться и потренироваться на вариантах двух прошлых лет.

Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по математике. Профильный уровень (pdf)

Пройдите первичное тестирование по демонстрационному варианту:

ПЕРВИЧНОЕ ТЕСТИРОВАНИЕ профильный уровень

Пожалуйста, подождите пока страница загрузится полностью.
Если эта надпись не исчезает долгое время, попробуйте обновить страницу. Этот тест использует javascript. Пожалуйста, влкючите javascript в вашем браузере.

If loading fails, click here to try again

Если Вы готовы, нажмите на кнопку "Начать". Желаем удачи!

Начать

Вы набрали %%PERCENTAGE%% баллов. %%RATING%%
Максимальное количество баллов, которое можно получить в этом тесте - 32.
%%PERCENTAGE%% от 32 - это ваш первичный балл.

Примерная шкала перевода первичных баллов ЕГЭ по математике 2021 профильного уровня

Первичный балл	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Тестовый балл	5	9	14	18	23	27	33	39	45	50	56	62	68	70	72	74
Первичный балл	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32
Тестовый балл	76	78	80	82	84	86	88	90	92	94	96	98	99	100	100	100

Рекомендуем Вам для более подробного изучения следующие материалы:
Задача №15 (C3), Задача №16 (С4), Задача №17 (С5), Задача №18 (С6), Задача №19 (С7).

Ваши ответы выделены серым.

Задание 1

Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?

Используйте виртуальную клавиатуру для ввода ответа:


A	30,5
B	8
C	7,5
D	12
E	5

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 1:

Между 23:50 дня отправления и 00:00 дня прибытия пройдёт 10 минут. Между 00:00 дня прибытия и 07:50 дня прибытия пройдёт 7 часов 50 минут. Следовательно, всего поезд будет в пути 7 часов 50 минут + 10 минут = 8 часов.

Ответ: 8.

Задание 2

На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указаны номера месяцев; по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией.

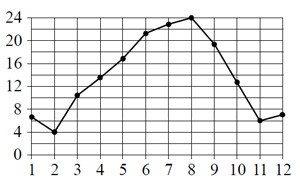Сколько месяцев средняя температура была больше 18 градусов Цельсия?

Используйте виртуальную клавиатуру для ввода ответа:


A	3
B	12
C	8
D	24
E	4

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 2:

По рисунку видно, что средняя температура в Сочи была больше 18 градусов Цельсия в 6-ом, 7-ом, 8-ом и 9-ом месяцах, то есть 4 месяца.

Ответ: 4.

Задание 3

На клетчатой бумаге с размером клетки 1 см x 1 см изображён треугольник. Найдите его площадь. Ответ дайте в см².

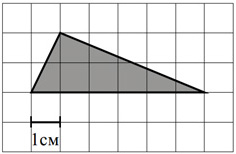
Используйте виртуальную клавиатуру для ввода ответа:


A	12
B	10
C	8
D	6
E	24

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 3:

$S=\frac{d_1 \cdot d_2}{2} =\frac{6 \cdot 2}{2}=6.$

Ответ: 6.

Задание 4

В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.

Используйте виртуальную клавиатуру для ввода ответа:


A	0,92
B	0,08
C	0,9
D	0,5
E	0,25

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 4:

$P = \frac{2}{25} = 0,08.$

Ответ: 0,08.

Задание 5

Найдите корень уравнения:

$3^{x-5}=81.$

Используйте виртуальную клавиатуру для ввода ответа:


A	27
B	9
C	4
D	3
E	5

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 5:

$3^{x-5}=3^4,$

$x-5=4,$

$x=5+4=9.$

Ответ: 9.

Задание 6

Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32 градусам. Найдите угол BOC. Ответ дайте в градусах.

Используйте виртуальную клавиатуру для ввода ответа:


A	90
B	64
C	58
D	16
E	32

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 6:

Угол, вписанный в окружность, равен половине соответствующего ему центрального угла:

$\angle BOC = 2 \cdot 32^{\circ} = 64^{\circ}.$

Ответ: 64.

Задание 7

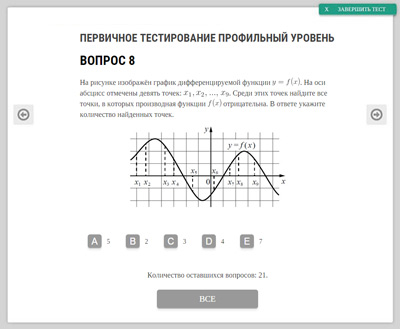
На рисунке изображён график дифференцируемой функции $y=f(x)$ . На оси абсцисс отмечены девять точек: $x_1 , x_2 , ..., x_9$ .

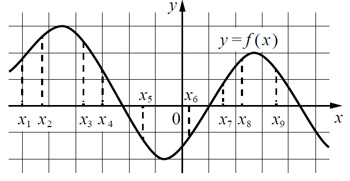
Найдите все отмеченные точки, в которых производная функции $f(x)$ отрицательна. В ответе укажите количество найденных точек.

Используйте виртуальную клавиатуру для ввода ответа:


A	2
B	7
C	4
D	3
E	5

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 7:

В тех точках, в которых производная функции отрицательна, функция убывает.
На данном графике это следующие точки: $x_3 , x_4 , x_5, x_9$ . Всего их 4.

Ответ: 4.

Задание 8

В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ выразите в см.

Используйте виртуальную клавиатуру для ввода ответа:


A	4
B	32
C	2
D	16
E	6

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 8:

$V_1 = S_1 \cdot h_1, V_2 = S_2 \cdot h_2,$

$d_2 = 2d_1 \Rightarrow S_2 = \frac {d^2}{4} = 4 S_1,$

$h_1 = 16, S_1 \cdot h_1 = S_2 \cdot h_2 \Rightarrow$

$\Rightarrow S_1 \cdot 16 = 4 \cdot S_1 \cdot h_2,$

$16 = 4 \cdot h_2, h_2 = 4.$

Ответ: 4.

Задание 9

Найдите $\sin 2\alpha$ , если $\cos\alpha = 0,6$ и $\pi < \alpha < 2\pi$ .

Используйте виртуальную клавиатуру для ввода ответа:


A	-0,96
B	0,81
C	-0,64
D	0,5
E	0,4

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 9:

$\sin^2\alpha = 1 - \cos^2\alpha,$

$\sin^2\alpha = 1 - 0,6^2 = 0,64.$

$\alpha\in\left( \pi; 2\pi \right) \Rightarrow$

$\Rightarrow \sin\alpha<0 \Rightarrow \sin\alpha = -0,8,$

$\sin2\alpha = 2 \sin\alpha\cdot \cos\alpha =2 \cdot ( -0,8) \cdot 0,6 =-0,96.$

Ответ: -0,96.

Задание 10

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением

$v = c \cdot \frac {f - f_0}{f + f_0},$

где c = 1500 м/с - скорость звука в воде; $f_0$ - частота испускаемого сигнала (в МГц); $f$ — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.

Используйте виртуальную клавиатуру для ввода ответа:


A	751
B	750
C	748
D	1501
E	479

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 10:

$v = c \cdot \frac {f - f_0}{f + f_0},$

$2 = 1500 \cdot \frac {f - 479}{f + 749},$

$1 = 750 \cdot \frac {f - 749}{f +749},$

$f +749 = 750 \cdot (f - 749),$

$f +749 = 750f - 749 \cdot 750,$

$f - 750f = -749 - 749 \cdot 750,$

$749f = 749 \cdot (750 + 1),$

$f = 751.$

Ответ: 751.

Задание 11

Весной катер идет против течения реки в $1\frac{2}{3}$ раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идет против течения в $1\frac{1}{2}$ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Используйте виртуальную клавиатуру для ввода ответа:


A	3
B	2
C	1
D	5
E	4

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 11:

1. Пусть $x$ — собственная скорость катера (км/ч), $y$ — скорость течения реки весной (км/ч).

2. Исходя из условия запишем отношение скоростей весной:

$\frac {x-y}{x+y}=\frac{3}{5};$

$5(x-y)=3(x+y);$

$x=4y.$ (1)

3. Исходя из условия запишем отношение скоростей летом:

$\frac {x-(y+1)}{x+(y+1)}=\frac{2}{3};$ .

$3(x-y-1)=2(x+y+1);$

$x=5y-5.$ (2)

4. Выразим у, приравняв правые части уравнений (1) и (2)

$4y=5y-5 => y=5.$

Ответ: 5.

Задание 12

Найдите точку максимума функции $y=ln(x+4)^2+2x+7$ .

Используйте виртуальную клавиатуру для ввода ответа:


A	4
B	-3
C	-8
D	-5
E	-9

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 12:

$y'=\frac{2}{x+4}+2.$

$\frac{2}{x+4}+2=0 \Rightarrow x = -5.$

Искомая точка максимума $x = -5.$

Ответ: -5.

Задание 13

а) Решите уравнение $\cos 2x=1-\cos\left ( \frac{\pi}{2} - x \right).$

б) Найдите все корни этого уравнения, принадлежащие промежутку $\left [ -\frac{5\pi}{2}; -\pi \right ).$

Используйте виртуальную клавиатуру для ввода ответа:


A	а) $\pi n,$ $n \in \mathbb{Z};$ $(-1)^k \frac {\pi}{6}+ \pi k, k \in \mathbb{Z};$ б) $-2 \pi;$ $- \frac{11 \pi}{6};$ $- \frac {7 \pi}{6}.$
B	а) $\pi n,$ $(-1)^n \frac {\pi}{6}+ \pi n,$ $n \in \mathbb{Z};$ б) $-2 \pi; - \frac{11 \pi}{6}.$
C	а) $\pi n,$ $n \in \mathbb{Z};$ $(-1)^k \frac {\pi}{6}+ \pi k, k \in \mathbb{Z};$ б) $\pi;$ $- \frac{11 \pi}{6};$ $- \frac {7 \pi}{6}.$
D	а) $2\pi n,$ $n \in \mathbb{Z};$ $(-1)^k \frac {5\pi}{6}+ \pi k, k \in \mathbb{Z};$ б) $-2 \pi;$ $- \frac{11 \pi}{6};$ $- \frac {7 \pi}{6}.$
E	а) $(-1)^k \frac {\pi}{6}+ \pi k,$ $k \in \mathbb{Z};$ б) $-2 \pi;$ $- \frac{11 \pi}{6};$ $- \frac {7 \pi}{6}.$

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 13:

а) Преобразуем обе части уравнения:

$1-2 \sin^2 x = 1 - \sin x,$

$2 \sin^2 x - \sin x = 0,$

$\sin x (2 \sin x -1 )=0,$

$\sin x = 0, \sin x = \frac{1}{2}.$

Из уравнения $\sin x = 0$ находим:

$x = \pi n, n \in \mathbb{Z}.$

Из уравнения $\sin x = \frac{1}{2}$ находим:

$x = (-1)^k \frac {\pi}{6}+ \pi k, k \in \mathbb{Z}.$

б) С помощью числовой окружности отберём корни уравнения, принадлежащие промежутку $\left [- \frac{5\pi}{2}; -\pi \right ).$

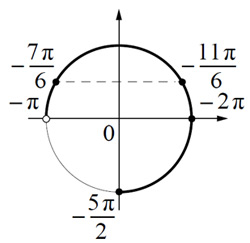
Получаем числа: $-2 \pi; - \frac{11 \pi}{6}; - \frac {7 \pi}{6}.$

Ответ:
а) $\pi n, n \in \mathbb{Z};$
$(-1)^k \frac {\pi}{6}+ \pi k, k \in \mathbb{Z};$
б) $-2 \pi; - \frac{11 \pi}{6}; - \frac {7 \pi}{6}.$

Задание 14

Все рёбра правильной треугольной призмы ABCA₁B₁C₁ имеют длину 6. Точки M и N — середины рёбер AA₁ и A₁C₁ соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB₁.

Используйте виртуальную клавиатуру для ввода ответа:


A	$\arcsin \frac{ \sqrt 3}{8}.$
B	$\arcsin \sqrt { \frac{3}{8}}.$
C	$\sin \frac{ \sqrt 3}{8}.$
D	$\arcsin \frac{3}{8}.$
E	$\arcsin \sqrt { \frac{1}{8}}.$

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 14:

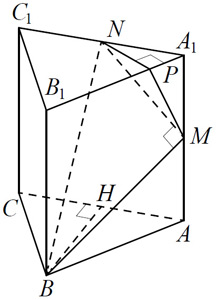
а) Пусть точка H — середина AC.

Тогда $BN^2 = BH^2 + NH^2;$

$BN^2 =(3 \sqrt 3)^2 + 6^2;$

$BN^2 = 63.$

С другой стороны, $BM^2 + MN^2$ $= (3^2 + 6^2) + (3^2 + 3^2);$

$BM^2 + MN^2 = 63.$

Тогда по теореме, обратной теореме Пифагора, треугольник BMN является прямоугольным с прямым углом M.

б) Проведём перпендикуляр NP к прямой A₁B₁.

Тогда прямая NP перпендикулярна A₁B₁ и прямая NP перпендикулярна A₁A. Следовательно, прямая NP перпендикулярна ABB₁. Поэтому MP — проекция MN на плоскость ABB₁.

Прямая BM перпендикулярна MN, тогда по теореме о трёх перпендикулярах прямая BM перпендикулярна MP. Следовательно, угол NMP — линейный угол искомого угла.

Длина NP равна половине высоты треугольника A₁B₁C₁ , то есть $NP = \frac{3 \sqrt 3 }{2}.$

Поэтому $\sin \angle NMP = \frac {NP}{MN} = \frac{3 \sqrt 3 }{2 \cdot 3 \sqrt 2} = \frac {\sqrt 3 }{\sqrt 8}.$

Следовательно, $\angle NMP = \arcsin \sqrt { \frac{3}{8}}.$

Ответ: б) $\arcsin \sqrt { \frac{3}{8}}.$

Задание 15

Решите неравенство:

$\frac{9^x - 2 \cdot 3^{x+1}+4}{3^x-5} + \frac{2\cdot 3^{x+1} -51}{3^x-9} \le 3^x + 5.$

Используйте виртуальную клавиатуру для ввода ответа:


A	$\left ( -\infty; log_{3}{5} \right ); \left ( log_{3}{5}; +\infty \right )$
B	$\left (1; log_{3}{5} \right )$
C	$\left ( -\infty; 1 \right ]; \left ( log_{3}{5};2 \right )$
D	$\left ( -\infty; 1 \right ); \left ( log_{3}{5}; +\infty \right )$
E	$\left ( -\infty; \frac{1}{3} \right ]; \left ( log_{3}{5};2 \right )$

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 15:

Пусть $t = 3^x$ ,

тогда неравенство примет вид:

$\frac{t^2 - 6t+4}{t-5} + \frac{6t -51}{t-9} \le t + 5$ ,

$\frac{(t-1)(t-5)}{t-5} - \frac{1}{t-5} + \frac{6(t -9)}{t-9} + \frac{3}{t-9} \le t + 5$ ,

$- \frac{1}{t-5} + \frac{3}{t-9} \le 0$ ,

$\frac{t - 3}{(t-5)(t-9)} \le 0$ ,

откуда:

$t \le 3; 5 < t < 9$ .

При $t \le 3$ получим $3^x \le 3, x \le 1.$

При $5 < t < 9$ получим $5 < 3^x < 9, log_{3}{5} < x < 2.$

Ответ: $\left ( -\infty; 1 \right ]; \left ( log_{3}{5};2 \right )$

Задание 16

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Используйте виртуальную клавиатуру для ввода ответа:


A	3,2
B	1,6
C	4,0
D	12
E	0,8

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 16:

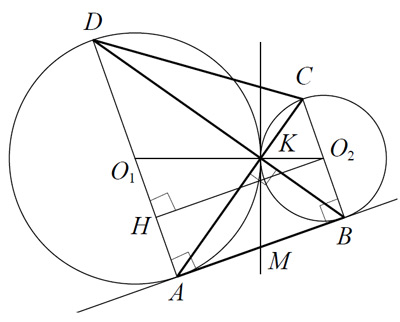
а) Обозначим центры окружностей O₁ и O₂ соответственно.

Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке M. По свойству касательных, проведённых из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный.

Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD и AB перпендикулярны. Аналогично, получаем, что BC перпендикулярна AB. Следовательно, прямые AD и BC параллельны.

б) Пусть, для определённости, первая окружность имеет радиус 4, а вторая — радиус 1.

Треугольники BKC и AKD подобны,

$\frac {AD}{BC} = 4.$

Пусть $S_{BKC} = S$ , тогда $S_{AKD} = 16S.$

У треугольников AKD и AKB общая высота, следовательно,

$\frac {S_{AKD}}{S_{AKB}} = \frac {DK}{KB} = \frac {AD}{BC}.$

То есть $S_{AKB}=4S$ . Аналогично, $S_{CKD}=4S.$

Площадь трапеции ABCD равна 25S .

Вычислим площадь трапеции ABCD. Проведём к AD перпендикуляр O₂H, равный высоте трапеции, и найдём его из прямоугольного треугольника O₂HO₁ :

$O_2H = \sqrt{O_1O_2^2-O_1H^2}=4.$

Тогда

$S_{ABCD} = \frac{AD+BC}{2} \cdot O_2H,$

$S_{ABCD} = \frac{8+2}{2} \cdot 4 = 20.$

Следовательно, 25S = 20 , откуда S = 0,8 и $S_{AKB} = 4S = 3,2$ .

Ответ: 3,2.

Задание 17

15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы: − 1-го числа месяца долг увеличивается на r% по сравнению с концом предыдущего месяца, где r целое число. − Со 2 по 14 число необходимо выплатить часть долга. − 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии с таблицей.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в млн рублей)	1	0,6	0,4	0,3	0,2	0,1	0

Дата	Долг (в млн рублей)
15.01	1
15.02	0,6
15.03	0,4
15.04	0,3
15.05	0,2
15.06	0,1
15.07	0

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.

Используйте виртуальную клавиатуру для ввода ответа:


A	7
B	8
C	9
D	7,5
E	7,6

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 17:

Долг перед банком (в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:

1; 0.6; 0.4; 0.3; 0.2; 0.1; 0.

Пусть $k =1 + \frac{r}{100},$

тогда долг на первое число каждого месяца равен:

$k; 0.6k; 0.4k; 0.3k; 0.2k; 0.1k.$

Следовательно, выплаты со 2-го по 14-е число каждого месяца составляют:

$k - 0,6; 0,6k - 0,4; 0,4k - 0,3; 0,3k - 0,2; 0,2k - 0,1; 0,1k.$

Общая сумма выплат составляет:

$k (1 + 0,6 + 0,4 + 0,3 + 0,2 + 0,1) - (0,6 + 0,4 + 0,3 + 0,2 + 0,1) = (k - 1)(1 + 0,6 + 0,4 + 0,3 + 0,2 + 0,1) + 1 = 2,6(k - 1) + 1.$

По условию, общая сумма выплат будет меньше 1,2 млн рублей, значит,

$2,6(k - 1) + 1 < 1,2;$

$2,6\cdot\frac{r}{100}+ 1 < 1,2;$

$r < 7\frac{9}{13}.$

Наибольшее целое решение этого неравенства — число 7. Значит, искомое число процентов — 7.

Ответ: 7.

Задание 18

Найдите все положительные значения $a$ , при каждом из которых система

$\left\{ \begin{aligned} &\left( |x| - 5 \right )^2 + (y - 4)^2 = 9,\\ &(x + 2)^2 + y^2 = a^2\\ \end{aligned} \right.$

имеет единственное решение.

Используйте виртуальную клавиатуру для ввода ответа:


A	$2; 3\sqrt{5} + 3.$
B	$\left (2; 3\sqrt{5} + 3 \right ].$
C	$2; \left (3\sqrt{5} - 3; 3\sqrt{5} + 3 \right ).$
D	$\left [ 2; 3\sqrt{5} - 3 \right ].$
E	$2; \sqrt{65} + 3.$

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 18:

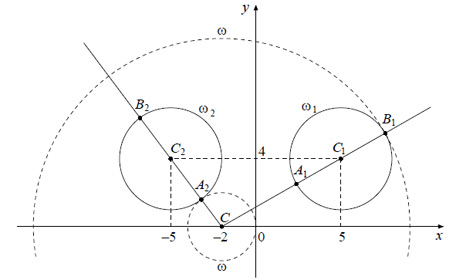
Если $x \ge 0$ , то уравнение $\left ( |x| - 5 \right )^2 + (y - 4)^2 = 9$ задаёт окружность $\omega_1$ с центром в точке $C_1(5; 4)$ радиуса 3, а если $x < 0$ , то оно задаёт окружность $\omega_2$ с центром в точке $C_2(-5; 4)$ того же радиуса (см. рис.).

При положительных значениях параметра $a$ уравнение $(x +2)^2 + y^2 = a^2$ задаёт окружность $\omega$ с центром в точке $C(-2; 0)$ радиуса $a$ . Поэтому задача состоит в том, чтобы найти все значения параметра $a$ , при каждом из которых окружность $\omega$ имеет единственную общую точку с объединением окружностей $\omega_1$ и $\omega_2$ .

Из точки $C$ проведём луч $CC_1$ и обозначим $A_1$ и $B_1$ точки его пересечения с окружностью $\omega_1,$ где $A_1$ лежит между $C$ и $C_1$ . Так как $CC_1 = \sqrt{(5 +2)^2 + 4^2},$ $CC_1 = \sqrt {65},$ то $CA_1 = \sqrt {65} - 3,$ $CB_1 = \sqrt {65} + 3$ .

При $a < CA_1$ или $a > CB_1$ окружности $\omega$ и $\omega_1$ не пересекаются.

При $CA_1 < a < CB_1$ окружности $\omega$ и $\omega_1$ имеют две общие точки.

При $a = CA_1$ или $a = CB_1$ окружности $\omega$ и $\omega_1$ касаются.

Из точки $C$ проведём луч $CC_2$ и обозначим $A_2$ и $B_2$ точки его пересечения с окружностью $\omega_2,$ где $A_2$ лежит между $C$ и $C_2$ . Так как $CC_2 = \sqrt{(-5 +2)^2 + 4^2},$ $CC_2 = 5,$ то $CA_2 = 5 - 3=2,$ $CB_2 = 5 + 3=8.$

При $a < CA_2$ или $a > CB_2$ окружности $\omega$ и $\omega_2$ не пересекаются.

При $CA_2 < a < CB_2$ окружности $\omega$ и $\omega_2$ имеют две общие точки.

При $a = CA_2$ или $a = CB_2$ окружности $\omega$ и $\omega_2$ касаются.

Исходная система имеет единственное решение тогда и только тогда, когда окружность $\omega$ касается ровно одной из двух окружностей $\omega_1$ и $\omega_2$ и не пересекается с другой. Так как $CA_1 < CA_2 < CB_1 < CB_2,$ то условию задачи удовлетворяют только числа $a = 2$ и $a = \sqrt {65} +3$ .

Ответ: $2; \sqrt{65} + 3$ .

Задание 19

На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно −3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно −8.

а) Сколько чисел написано на доске?

б) Каких чисел написано больше: положительных или отрицательных?

в) Какое наибольшее количество положительных чисел может быть среди них?

Используйте виртуальную клавиатуру для ввода ответа:


A	а) 36; б) отрицательных; в) 16
B	а) 40; б) положительных; в) 16
C	а) 44; б) отрицательных; в) 17
D	а) 35; б) положительных; в) 15
E	а) 40; б) отрицательных; в) 20

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 19:

Пусть среди написанных чисел k положительных, l отрицательных и m нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому $4k-8l+0m = -3(k+l+m).$

а) Заметим, что в левой части каждое слагаемое делится на 4, поэтому $k + l + m$ — количество целых чисел — делится на 4. По условию $40 < k + l + m < 48$ , поэтому $k + l + m = 44$ . Таким образом, написано 44 числа.

б) Приведём равенство $4k-8l = -3(k+l+m)$ к виду $5l = 7k + 3m$ . Так как $m \geq 0$ , получаем, что $5l \geq 7k$ , откуда $l > k$ . Следовательно, отрицательных чисел больше, чем положительных.

в) (оценка) Подставим $k + l + m = 44$ в правую часть равенства $4k-8l=-3(k+l+m);$ $4k-8l=-132$ , откуда $k=2l-33$ . Так как $k + l \leq 44$ , получаем: $3l-33 \leq 44 , 3l \leq 77,$ $l \leq 25, k=2l-33 \leq 17:$ то есть положительных чисел не более 17.

в) (пример) Приведём пример, когда положительных чисел ровно 17.

Пусть на доске 17 раз написано число 4, 25 раз написано число −8 и два раза написан 0. Тогда $\frac{4 \cdot 17 -8 \cdot 25}{44}=-3$ , указанный набор удовлетворяет всем условиям задачи.

Ответ: а) 44; б) отрицательных; в) 17.

Если вы закончили, то нажмите кнопку ниже. Все вопросы, на которые вы не ответили будут отмечены знаком "Ошибка". Завершить тестирование

Количество оставшихся заданий: 19.

←

Все

→

Закрашенные квадратики - это завершенные задания.

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	Конец

Демонстрационный вариант ЕГЭ по математике 2019 года профильного уровня с решением

ПЕРВИЧНОЕ ТЕСТИРОВАНИЕ профильный уровень

Навигация