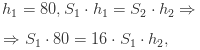Вход

X

Демонстрационный вариант ЕГЭ по математике 2020 года базового уровня с решением

12 Март 2020 Главная страница » Подготовка к ЕГЭ Просмотров: 2572

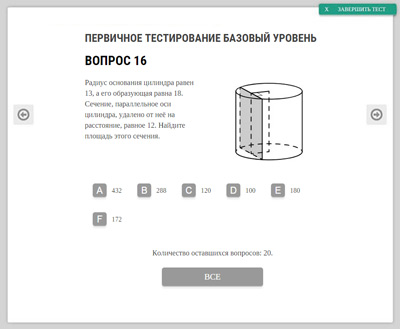
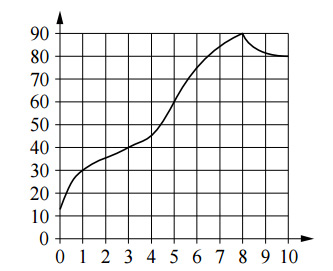
Демонстрационный вариант экзаменационной работы базового уровня 2020 года по содержанию и структуре не отличается от вариантов предыдущих лет, поэтому для подготовки к экзамену 2020 года рекомендуем Вам также ознакомиться со всеми вариантами, доступными на нашем сайте.
Внимательно прочитайте пояснения, которые даются к демонстрационному варианту — оно содержит важную информацию: сколько баллов дается за выполнение заданий, как правильно заполнять бланки ответов, сколько времени отводится на решение всей работы и т.п. Вы можете скачать демонстрационные варианты ЕГЭ по математике базового уровня в формате pdf:

Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2020 года по математике. Базовый уровень (pdf)

Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2019 года по математике. Базовый уровень (pdf)

Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2018 года по математике. Базовый уровень (pdf)

Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2017 года по математике. Базовый уровень (pdf)

Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2016 года по математике. Базовый уровень (pdf)

Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2016 года по математике. Базовый уровень — ПРОЕКТ (pdf)

Пройдите первичное тестирование по демонстрационному варианту онлайн:

ПЕРВИЧНОЕ ТЕСТИРОВАНИЕ базовый уровень

Пожалуйста, подождите пока страница загрузится полностью.
Если эта надпись не исчезает долгое время, попробуйте обновить страницу. Этот тест использует javascript. Пожалуйста, влкючите javascript в вашем браузере.

If loading fails, click here to try again

Если Вы готовы, нажмите на кнопку "Начать". Желаем удачи!

Начать

Вы правильно ответили на %%SCORE%% вопросов. Ваша оценка - %%RATING%%.

Шкала перевода баллов единого государственного экзамена по математике базового уровня в отметку по пятибалльной шкале

Отметка по пятибалльной шкале	«2» (неудовлетворит.)	«3» (удовлетворит.)	«4» (хорошо)	«5» (отлично)
Общий балл	0-6	7-11	12-16	17-20

Ваши ответы выделены серым.

Задание 1

Найдите значение выражения

$(\frac{1}{3}+\frac{1}{5})\cdot6.$

Используйте виртуальную клавиатуру для ввода ответа:


A	3
B	16
C	3,2
D	4,8
E	2,5
F	48

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 1:

$(\frac{1}{3}+\frac{1}{5})\cdot6=\frac{8\cdot6}{15}=\frac{8\cdot6}{15}=3,2$

Ответ: 3,2.

Задание 2

Найдите значение выражения

$\frac{0,24\cdot10^6}{0.6\cdot10^4}.$

Используйте виртуальную клавиатуру для ввода ответа:


A	60
B	4
C	0,04
D	40
E	0,4
F	400

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 2:

$\frac{0,24\cdot10^6}{0.6\cdot10^4}=0,4\cdot10^2=40.$

Ответ: 40.

Задание 3

ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике?

Используйте виртуальную клавиатуру для ввода ответа:


A	100
B	50
C	55
D	25
E	75
F	5

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 3:

Общее количество выпускников:

$25\cdot3=75.$

Вычтем из общего количества учеников тех, кто сдавал экзамен:

$75-25=50.$

Ответ: 50.

Задание 4

Найдите m из равенства F = ma, если F = 84 и a = 12.

Используйте виртуальную клавиатуру для ввода ответа:


A	7
B	9
C	98
D	72
E	8
F	70

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 4:

$m = \frac{F}{a} = \frac{84}{12} = 7.$

Ответ: 7.

Задание 5

Найдите $\cos \alpha$ , если $\sin \alpha = 0.8$ , и $90^{\circ} < \alpha < 180^{\circ}$ .

Используйте виртуальную клавиатуру для ввода ответа:


A	0,9
B	-0,36
C	0,6
D	-0,6
E	-0,2
F	0,36

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 5:

$\cos^2\alpha = 1 - \sin^2\alpha ,$

$\cos^2\alpha = 1 - 0,8^2 = 0,36.$

$90^{\circ} < \alpha < 180^{\circ}\Rightarrow$

$\Rightarrow \cos\alpha<0, \cos\alpha = -0,6.$

Ответ: -0,6.

Задание 6

Баночка йогурта стоит 14 рублей 60 копеек. Какое наибольшее количество баночек йогурта можно купить на 100 рублей?

Используйте виртуальную клавиатуру для ввода ответа:


A	7
B	6,8
C	2
D	6
E	7,8
F	1,4

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 6:

$\frac{100}{14,6} = 6,8.$

Округлив до целого числа в меньшую сторону, получим, что на 100 рублей можно купить не больше 6-ти баночек йогурта.

Ответ: 6.

Задание 7

Найдите корень уравнения

$3^{x-3}=81.$

Используйте виртуальную клавиатуру для ввода ответа:


A	30
B	1
C	12
D	7
E	4
F	6

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 7:

$3^{x-3}=3^4,$

$x-3=4,$

$x=7.$

Ответ: 7.

Задание 8

Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.

Используйте виртуальную клавиатуру для ввода ответа:


A	90
B	140
C	120
D	125
E	135
F	75

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 8:

Периметр участка:

$30\cdot2 + 25\cdot2= 60 + 50=110.$

Длина забора внутри участка - 25 м. Общая длина забора:

$110 + 25 = 135.$

Ответ: 135.

Задание 9

Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

Величины	Возможные значения
А) рост ребёнка	1) 32 км
Б) толщина листа бумаги	2) 30 м
В) длина автобусного маршрута	3) 0,2 мм
Г) высота жилого дома	4) 110 см

В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.

Ответ:

A	Б	В	Г

Используйте виртуальную клавиатуру для ввода ответа:


A	4321
B	4231
C	3421
D	3214
E	4213
F	4312

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 9:

А) рост ребёнка - 110 см.

Б) толщина листа бумаги - 0,2 мм.

В) длина автобусного маршрута - 32 км.

Г) высота жилого дома - 30 м.

A	Б	В	Г
4	3	1	2

Ответ: 4312.

Задание 10

В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из России.

Используйте виртуальную клавиатуру для ввода ответа:


A	0,2
B	7
C	0,25
D	12
E	23
F	5

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 10:

$P = \frac{7}{35} = 0,2.$

Ответ: 0,2.

Задание 11

На диаграмме приведены данные о длине восьми крупнейших рек России (в тысячах километров). Первое место по длине занимает Лена. На каком месте по длине, согласно этим данным, находится Амур?

Используйте виртуальную клавиатуру для ввода ответа:


A	7
B	6
C	8
D	1
E	2
F	3

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 11:

По рисунку видно, что длина Амура меньше, чем длины Лены, Иртыша, Оби, Волги, Енисея и Нижней Тунгуски, то есть Амур занимает 7-ое место по длине.

Ответ: 7.

Задание 12

Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.

Номер переводчика	Языки	Стоимость услуг (руб. в день)
1	Немецкий, испанский	7000
2	Английский, немецкий	6000
3	Английский	3000
4	Английский, французский	6000
5	Французский	2000
6	Испанский	4000

Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день. В ответе укажите ровно один набор номеров переводчиков без пробелов, запятых и других дополнительных символов.

Используйте виртуальную клавиатуру для ввода ответа:


A	2
B	256
C	134
D	125
E	14
F	165

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 12:

Представим данные в таблице, в которой 2 столбца. В первом - возможные сочетания номеров переводчиков, представляющих все 4 языка. Во втором - общая стоимость услуг.

1, 4	7 000 + 6 000 = 13 000
2, 5, 6	6 000 + 2 000 + 4 000 = 12 000
1, 3, 4	7 000 + 3 000 + 6 000 = 16 000
1, 3, 5	7 000 + 3 000 + 2 000 = 12 000
1, 2, 5	7 000 + 6 000 + 2 000 = 15 000

Видно, что условию удовлетворяют два варианта: 256 и 135. Любой из них можно записать в ответ.

Ответ: 256.

Задание 13

В сосуд цилиндрической формы налили воду до уровня 80 см. Какого уровня достигнет вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у первого? Ответ дайте в сантиметрах. первичное тестирование

Используйте виртуальную клавиатуру для ввода ответа:


A	48
B	5
C	20
D	4
E	40
F	16

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 13:

$V_1 = S_1 \cdot h_1, V_2 = S_2 \cdot h_2,$

$d_2 = 4d_1 \Rightarrow S_2 = \frac {d^2}{4} = 16 S_1,$

$h_1 = 80,$ $S_1 \cdot h_1 = S_2 \cdot h_2 \Rightarrow S_1 \cdot 80 = 16 \cdot S_1 \cdot h_2,$

$80 = 16 \cdot h_2,$ $h_2 = 5.$

Ответ: 5.

Задание 14

На графике показано изменение температуры в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси — температура двигателя в градусах Цельсия.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.

Интервалы времени	Характеристики процесса
А) 0–1 мин.	1) самый медленный рост температуры
Б) 1–3 мин.	2) температура падала
В) 3–6 мин.	3) температура находилась в пределах от 40°C до 80°C
Г) 8–10 мин.	4) температура не превышала 30°C

В таблице под каждой буквой, соответствующей интервалу времени, укажите номер характеристики процесса.

Ответ:

A	Б	В	Г

Используйте виртуальную клавиатуру для ввода ответа:


A	4312
B	4132
C	3241
D	3142
E	4321
F	4123

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 14:

По графику видно, что с 0 по 1 минуту температура не превышала 30°C, со 1 по 3 минуты - росла медленнее всего, с 3 по 6 минуты - находилась в пределах от 40°C до 80°C, а с 8 по 10 минуты - падала.

A	Б	В	Г
4	1	3	2

Ответ: 4132.

Задание 15

В треугольнике ABC угол ACB равен 90°, cos B = 0,8, AC = 4. Отрезок CH - высота треугольника ABC (см. рисунок). Найдите длину отрезка AH.

Используйте виртуальную клавиатуру для ввода ответа:


A	5
B	2
C	2,5
D	3,2
E	4
F	3,6

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 15:

Рассмотрим треугольник АНС. В нём АС – гипотенуза, АН – искомый катет, прилежащий к углу А.

$\cos A = \frac{AH}{AC},$

$AH = AC \cdot \cos A ,$

$AH = 4 \cdot 0.8 = 3.2.$

Ответ 3.2.

Задание 16

Радиус основания цилиндра равен 13, а его образующая равна 18. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.

Используйте виртуальную клавиатуру для ввода ответа:


A	180
B	120
C	432
D	172
E	100
F	288

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 16:

Сечение представляет из себя прямоугольник, одна сторона которого известна - это образующая цилиндра, равная 18:

$a = 18.$

Половину второй стороны найдем по теореме Пифагора из треугольника, образованного радиусом основания и отрезком, равным расстоянию от оси цилиндра до сечения:

$\frac{b}{2}= \sqrt{13^2-12^2}=5,$

$b = 10,$

$s = a\cdot b = 18 \cdot 10 = 180.$

Ответ: 180.

Задание 17

На прямой отмечены точки A, B, C и D.

Установите соответствие между указанными точками и числами из правого столбца, которые им соответствуют.

ТОЧКИ	ЧИСЛА
A	1) $\log_{2}10$
B	2) $\frac{7}{3}$
C	3) $\sqrt{26}$
D	4) $(\frac{3}{5})^{-1}$

Ответ:

A	B	C	D

Используйте виртуальную клавиатуру для ввода ответа:


A	4213
B	4132
C	4321
D	3412
E	3142
F	3241

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 17:

1) $\log_{2}8 < \log_{2}10 < \log_{2}16,$

$3 < \log_{2}10 < 4.$

Соответствует точке C.

2) $\frac{6}{3} < \frac{7}{3} < \frac{9}{3}$

$2 < \frac{7}{3} < 3.$

Соответствует точке B.

3) $\sqrt{25} < \sqrt{26} < \sqrt{36}$

$5 < \sqrt{26} < 6.$

Соответствует точке D.

4) $0.6^{-1} = \frac{10}{6} = 1\frac{4}{6}.$

Соответствует точке A.

Занесем данные в таблицу:

A	B	C	D
4	2	1	3

Ответ: 4213.

Задание 18

В классе учится 20 человек, из них 13 человек посещают кружок по истории, а 10 — кружок по математике. Выберите утверждения, которые верны при указанных условиях.

Каждый ученик этого класса посещает оба кружка.
Найдутся хотя бы двое из этого класса, кто посещает оба кружка.
Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике.
Не найдётся 11 человек из этого класса, которые посещают оба кружка.

В ответе укажите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Используйте виртуальную клавиатуру для ввода ответа:


A	4
B	21
C	24
D	13
E	234
F	2

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 18:

Каждый ученик этого класса посещает оба кружка. Нет, в исходных данных нет такой информации.
Найдутся хотя бы двое из этого класса, кто посещает оба кружка. Да, даже если половина класса (10 человек) посещает один кружок, и вторая половина (10 человек) - другой, то из 13 человек 3 обязательно будут посещать оба кружка.
Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике. Нет, если половина класса (10 человек) посещает кружок по математике, то вторая половина (10 человек из 13) может посещать кружок по истории, и не посещать кружок по математике.
Не найдётся 11 человек из этого класса, которые посещают оба кружка. Да, кружок по математике посещают только 10 человек, а значит не может быть 11 человек, посещающих оба кружка.

Задание 19

Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.

Используйте виртуальную клавиатуру для ввода ответа:


A	497
B	397
C	587
D	398
E	589
F	299

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 19:

Решим задачу методом подбора. Рассмотрим следующие цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Мы не можем использовать 0, потому что из оставшихся двух цифр нельзя получить 20.

Мы не можем использовать 1, так как из оставшихся двух цифр нельзя получить 19.

Из других цифр можно составить такие наборы:

2 + 9 + 9;
3 + 9 + 8;
4 + 9 + 7;
4 + 8 + 8;
5 + 9 + 6;
5 + 8 + 7.

Это всё, других способов представления числа 20 нет. Все 6 наборов соответствуют первому условию.

Теперь надо проверить второе условие: сумма квадратов делится на 3. «Признак делимости на 3»: число делится на 3, если сумма его цифр делится на 3.

Найдём сумму квадратов и проверим её делимость на 3:

4+81+81=166 1+6+6 =13 не делится на 3;
9+81+64=154 1+5+4=10 не делится на 3;
16+81+49=146 1+4+6=11 не делится на 3;
16+64+64=144 1+4+4=9 делится на 3;
25+81+36=142 1+4+2=7 не делится на 3;
25+64+49=138 1+3+8=12 делится на 3.

Второму условию удовлетворяют два двузначных числа 4) 488 и 6) 587. Проверим третье условие – делится ли сумма квадратов на 9:

4. 144 / 9 = 16 (делится);
6. 138 / 9 = 15,(3) (в целых числах не делится).

Таким образом, всем трём условиям удовлетворяет только число 587.

Ответ: 587.

Задание 20

В обменном пункте можно совершить одну из двух операций:
• за 2 золотых монеты получить 3 серебряных и одну медную;
• за 5 серебряных монет получить 3 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. Насколько уменьшилось количество серебряных монет у Николая?

Используйте виртуальную клавиатуру для ввода ответа:


A	10
B	20
C	25
D	12
E	5
F	15

Так будет записан Ваш ответ в бланке:

Пояснение к заданию 20:

Пусть первая операция была совершена х раз (получили x медных монет), вторая операция у раз (получили у медных монет), тогда составим систему уравнений:

2х = 3у;
х=1,5у.

Общее количество операций:

х + у = 50;
1,5у + у = 50;
2,5у = 50;
у = 20.

Первая операция была проделана:

$x = 20\cdot 1.5 = 30$ раз.

Получено 90 серебряных монет.

Вторая операция проделана 20 раз (у = 20).
Получено 100 серебряных монет.

Количество серебряных монет у Николая уменьшилось на 100-90 = 10 монет.

Ответ: 10.

Если вы закончили, то нажмите кнопку ниже. Все вопросы, на которые вы не ответили будут отмечены знаком "Ошибка". Завершить тестирование

Количество оставшихся заданий: 20.

←

Все

→

Назад

Закрашенные квадратики - это завершенные задания.

1	2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20
Конец

Назад

Последние публикации:

Демонстрационный вариант ЕГЭ по математике 2020 года базового уровня с решением

ПЕРВИЧНОЕ ТЕСТИРОВАНИЕ базовый уровень

Навигация